47 Behavioural game theory exercises
47.1 Penalty kick
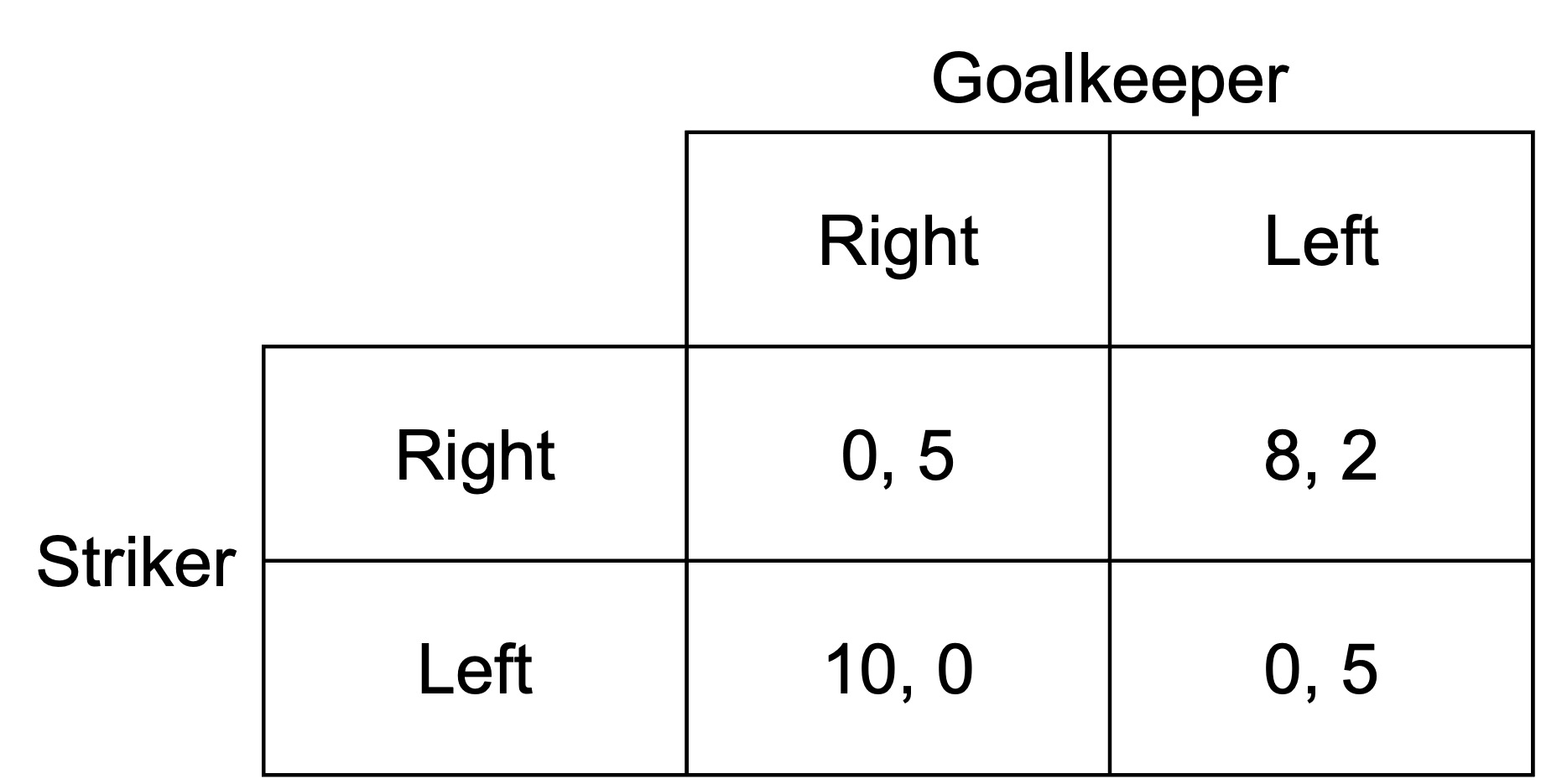
A soccer player (the striker) has a penalty kick. The striker is deciding whether to kick to the left or right. If the goalkeeper dives in the correct direction, the goalkeeper will stop the ball and the two sides will tie. Otherwise, the striker will score a goal and win.
Lately, the striker has been having trouble kicking to the right, sometimes missing the goals even when the goalkeeper doesn’t dive in that direction.
The expected payoffs for each combination of actions are as follows, with the payoff (x,y) being the payoffs for the striker and goalkeeper respectively:
Are there any pure-strategy Nash equilibria? If so, what are they?
There are no pure-strategy Nash equilibria. Whatever the striker does, the goalkeeper wants to match. If the goalkeeper matches, the striker wants to change.
a) Suppose the striker and goalkeeper are level-k thinkers.
If they were level-0, both would choose right or left with equal probability.
What would each player do if they were a level-1 thinker? Explain.
A level-1 striker will assume they are playing a level-0 goalkeeper.
They will estimate the the payoff from each action responding to the random play of a level-0 goalkeeper.
\begin{align*} E[U_S(R)]&=0.5\times 0+0.5\times 8 \\ &=4 \\ \\ E[U_S(L)]&=0.5\times 10+0.5*\times 0 \\ &=5 \end{align*}
The level-1 striker has a higher expected payoff for kicking left, so kick left.
A level-1 goalkeeper will assume they are playing a level-0 striker.
They will estimate the the payoff from each action responding to the random play of a level-0 striker.
\begin{align*} E[U_G(R)]&=0.5\times 5+0.5\times 0 \\ &=2.5 \\ \\ E[U_G(L)]&=0.5\times 2+0.5*\times 5 \\ &=3.5 \end{align*}
The level-1 goalkeeper has a higher expected payoff for going left, so go left.
b) What would each player do if they were a level-2 thinker? Explain.
A level-2 striker will assume they are playing a level-1 goalkeeper.
They believe the level-1 goalkeeper will go left, so they will go right (payoff 8 compared to payoff 0).
A level-2 goalkeeper will assume they are playing a level-1 striker.
They believe the level-1 striker will go left, so they will go left (payoff 5 compared to payoff 0).
47.2 Hide and seek
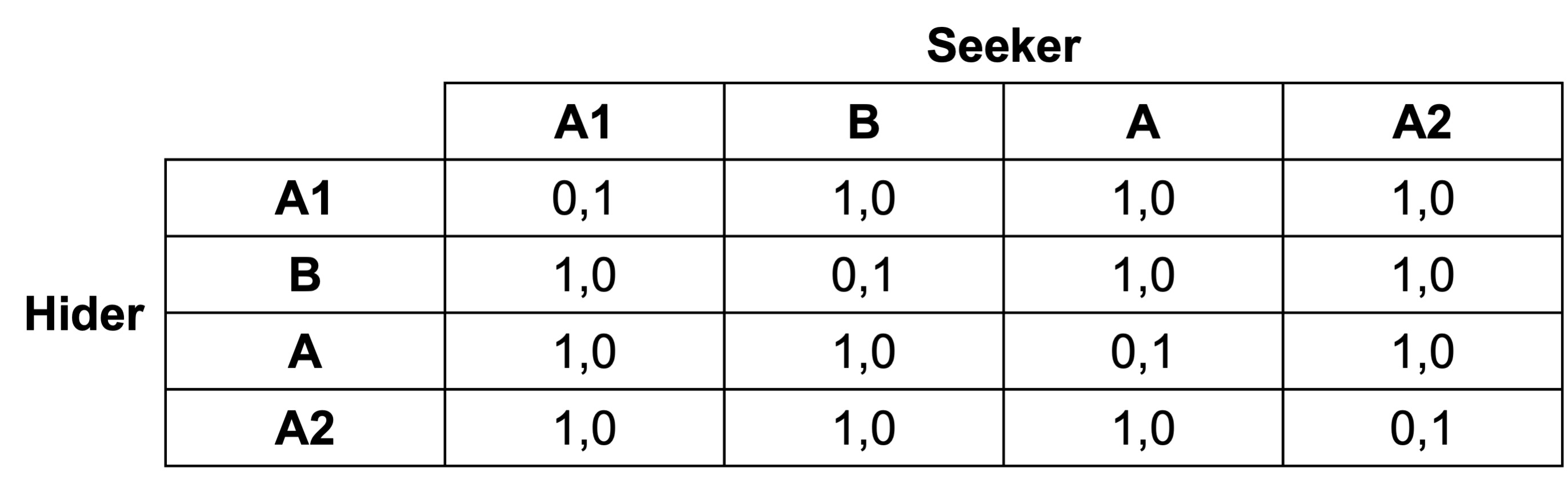
In the hide-and-seek game, the Hider selects one of the four boxes marked A, B, A and A. The Seeker guesses the box selected by the hider.
The Seeker wins if they find the Hider. Otherwise, the Hider wins.
The payoffs are as follows. I have labelled the end boxes A1 and A2 to distinguish the “A”s from each other.
Assume a level-0 seeker or hider selects a box by hiding in or looking in the “most salient” hiding spots. They choose A1 or A2 on the ends with p=0.3 each, or B (because it is different) with p=0.35. They hide or look in less salient middle A with probability 1−2\times 0.3−0.35=0.05.
(Note that this assumption for the level-0 agents is different to what we have assumed to date. We have typically assumed a level-0 agent randomly chooses an action.)
a) What box do the level-1 hider and seeker choose?
The level-1 hider calculates the expected payoff from hiding in each of the boxes if playing against a level-0 seeker.
\begin{align*} E[U(A1)]&=0×0.3+1×0.35+1×0.05+1×0.3=0.7 \\ \\ E[U(B)]&=1×0.3+0×0.35+1×0.05+1×0.3=0.65 \\ \\ E[U(A)]&=1×0.3+1×0.35+0×0.05+1×0.3=0.95 \\ \\ E[U(A2)]&=1×0.3+1×0.35+1×0.05+0×0.3=0.7 \end{align*}
The level-1 hider hides in the least salient box A.
The level-1 seeker calculates the expected payoff from looking in each of the boxes if playing against a level-0 hider.
\begin{align*} E[U(A1)]&=1×0.3+0×0.35+0×0.05+0×0.3=0.3 \\ \\ E[U(B)]&=0×0.3+1×0.35+0×0.05+0×0.3=0.35 \\ \\ E[U(A)]&=0×0.3+0×0.35+1×0.05+0×0.3=0.05 \\ \\ E[U(A2)]&=0×0.3+0×0.35+0×0.05+1×0.3=0.3 \end{align*}
The level-1 seeker looks in Box B.
If both the hider and seeker are level-1, the hider wins.
b) What box do the level-2 hider and seeker choose?
The level-2 hider knows that the level-1 seeker chooses B. They select any box apart from B with equal probability, all of which they believe will give a pay-off of 1.
The level-2 seeker knows that the level-1 hider will select A. They select A.
The level-2 seeker wins with probability 1/3.
c) What box do the level-3 hider and seeker choose?
The level-3 hider knows that the level-2 seeker chooses A. They select any box apart from A with equal probability, all of which they believe will give a pay-off of 1.
The level-3 seeker knows that the level-2 hider will select any box except B with equal probability. They select one of A1, A2 or A with equal probability.
The level-3 seeker wins with probability 1/3×1/3+1/3×1/3=2/9.
d) What box do the level-4 hider and seeker choose?
The level-4 hider knows that the level-3 seeker selected A1, A2 and A with equal probability. They select B.
The level-4 seeker knows that the level-3 hider selected any box apart from A with equal probability. They also select those boxes with equal probability.
The level-4 seeker wins with probability 1/3.
47.3 Matching pennies (with a twist)
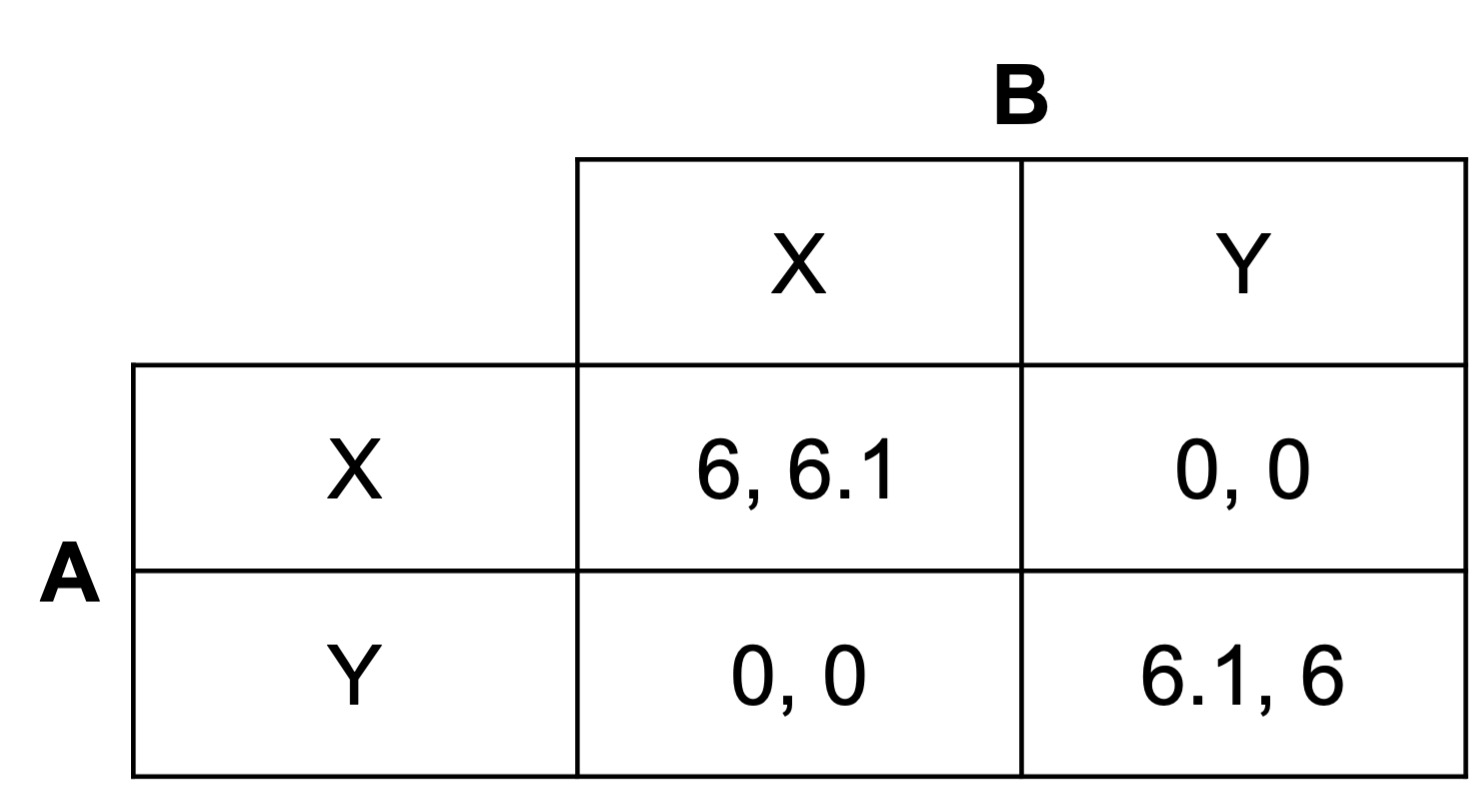
Consider the following two-player game:
a) What are the two pure-strategy Nash equilibria of this game?
The two pure-strategy Nash equilibria of this game are (X,X) and (Y,Y). That is, if the players are jointly playing either of those combinations of strategies, neither has an incentive to deviate. Their response is a best response to the other players’ actions.
b) Suppose players in this game think according to the level-k model. Assume a level-0 agent randomises between options with equal probability.
What would player A and player B do if they were level-1 players?
Remember the idea behind level-k thinking: given their own cognitive level, a player forms an expectation of what others will do and tries to be “one step ahead of them”.
We work out the utility of each option.
First, for player A:
\begin{align*} EU ^{1}_{A}(X)&= 0.5\times 6+0.5\times 0=3 \\ \\ EU ^{1}_{A}(Y)&= 0.5\times 0+0.5\times 6.1=3.05 \end{align*}
Player A chooses Y if they are a level-1 player.
Next, for player B:
\begin{align*} EU ^{1}_{B}(X)&= 0.5\times 6.1+0.5\times 0=3.05 \\ \\ EU ^{1}_{B}(Y)&= 0.5\times 0+0.5\times 6=3 \end{align*}
Player B chooses X if they are a level-1 player.
If both players are level-1, they will fail to coordinate.
c) What would player A and player B do if they were level-2 players?
We again work out the utility of each option:
First, for player A. They know that a level-1 player B will select X. Accordingly:
\begin{align*} EU^{2}_{A}(X)&=1\times 6+0\times 0=6 \\ \\ EU^{2}_{A}(Y)&=1\times 0+0\times 6.1=0 \end{align*}
Player A chooses X if they are a level-2 player.
Next, for player B. They know that a level-1 player A will select Y. Accordingly:
\begin{align*} EU ^{2}_{B}(X)&= 0\times 6.1+1\times0=0 \\ \\ EU ^{2}_{B}(Y)&= 0\times 0+1\times 6=6 \end{align*}
Player B chooses Y if they are a level-2 player.
If both players are level-2, they will fail to coordinate.
d) What would player A and player B do if they were level-3 players?
We again work out the utility of each option:
First, for player A. They know that a level-2 player B will select Y. Accordingly:
\begin{align*} EU ^{3}_{A}(X)&= 0\times 6+1\times 0=0 \\ \\ EU ^{3}_{A}(Y)&= 0\times 0+1\times 6.1=6.1 \end{align*}
Player A chooses Y if they are a level-3 player.
Next, for player B. They know that a level-2 player A will select X. Accordingly:
\begin{align*} EU ^{3}_{B}(X)&= 1\times 6.1+0\times 0=6.1 \\ \\ EU ^{3}_{B}(Y)&= 1\times 0+0\times 6=0 \end{align*}
Player B chooses X if they are a level-3 player.
If both players are level-3, they will fail to coordinate.
e) When this game is played in the laboratory, the players mis-coordinate. About 3/4 of the row players (player A) choose X while about 3/4 of the column players (player B) choose Y.
Of interest, each player tries to coordinate on the strategy that the other player would be better off coordinating on. That is, Player A receives 6 from successful coordination choosing X, which is less than the 6.1 Player A would get from coordinating on Y.
Given your answers to b) through d), what mix of level-k players might explain the mis-coordination described above?
That 3/4 of Player “A”s choose X and 3/4 of Player “B”s choose Y suggests there are many level-2 players (or possibly level-4). They each assume that the other player is level-1 and has picked the option with the highest payoff for themselves. They are effectively trying to coordinate with the other player by assuming that the other will seek their highest paying option. However, if both do this, both receive nothing.
47.4 Cafe
Two friends, Player 1 and Player 2, have arranged to meet at a cafe. Neither can remember which of the two cafes in town they had arranged to meet at.
Each player has a favourite cafe. However, they would prefer to go to their less-favourite cafe with a friend than go to their favourite cafe alone.
Each chooses a cafe and goes there. The payoffs for each combination of choices are in the table below, with the payoffs (x, y) being the payoffs for Player 1 and Player 2 respectively.
a) What are the pure-strategy Nash equilbria of this game?
If player 2 chooses cafe A, player 1 wants to choose cafe A.
If player 2 chooses cafe B, player 1 wants to choose cafe B.
If player 1 chooses cafe A, player 1 wants to choose cafe A.
If player 1 chooses cafe B, player 1 wants to choose cafe B.
The two pure-strategy Nash equilibria are (cafe A, cafe A) and (cafe B, cafe B).
b) What would Player 1 and Player 2 do if each was a level-1 thinker? Explain.
If Player 2 chooses randomly, Player 1’s payoff’s from each option are:
\begin{align*} U_1(\text{cafe A})&=0.5\times 2+0.5\times 0=1 \\[6pt] U_1(\text{cafe B})&=0.5\times 0+0.5\times 1=0.5 \end{align*}
Player 1 chooses cafe A.
If Player 1 chooses randomly, Player 2’s payoff’s from each option are:
\begin{align*} U_2(\text{cafe A})&=0.5\times 1+0.5\times 0=0.5 \\[6pt] U_2(\text{cafe B})&=0.5\times 0+0.5\times 3=1.5 \end{align*}
Player 2 chooses cafe B.
c) What would Player 1 and Player 2 do if each was a level-2 thinker? Explain.
The level-2 Player 1 assumes that Player 2 is level-1. Therefore, they assume that Player 2 will choose cafe B. Accordingly, they choose cafe B.
The level-2 Player 2 assumes that Player 1 is level-1. Therefore, they assume that Player 1 will choose cafe A. Accordingly, they choose cafe A.
47.5 Buying a car
Suppose that you are considering purchasing a car.
You believe that the seller values it between $1000 and $5000, with an equal probability that it has a value at any point in this range. That is, you believe it is uniformly valued to the seller between $1000 and $5000.
The seller knows the car and its true value.
Assume that whatever the car is worth to the seller, it is worth 1.33 times that to you (so a car worth $2400 to the owner is actually worth $3200 to you).
a) What offer should you make to ensure that you will not lose money?
Suppose you offer $x. If the seller accepts, the value must be between $1000 and $x.
As the value evenly distributed across that interval, its average value would be:
1000+\frac{x−1000}{2}=500+\frac{x}{2}
The expected value of the car to you will be:
\frac{4}{3}\bigg(500+\frac{x}{2}\bigg)
To ensure you don’t lose you want:
\frac{4}{3}\bigg(500+\frac{x}{2}\bigg)>x
Solving this out, you expect to make a profit where x<\$2000.
b) Suppose you are cursed player and you believe sellers will take the average optimal action of selling whenever they are offered more than $3000. As a result, you decide to offer $3000. What is your accepted profit if the seller accepts your offer?
If seller accepts, the value must be between $1000 and $3000.
If value evenly distributed across that interval, its average value would be $2000.
Given it is worth 1.33 times more to you, it would be worth $2,667 on average.
You would lose, on average, $333.
47.6 Advice
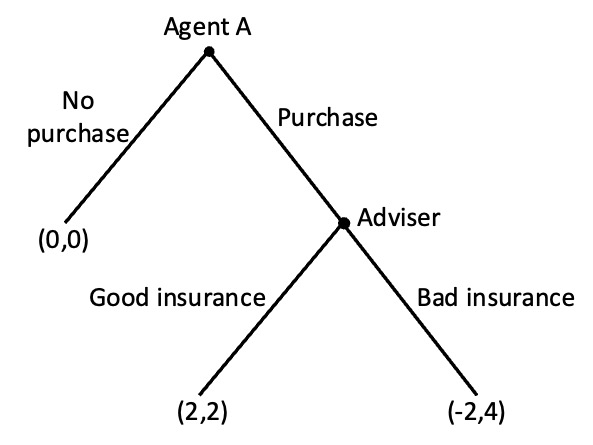
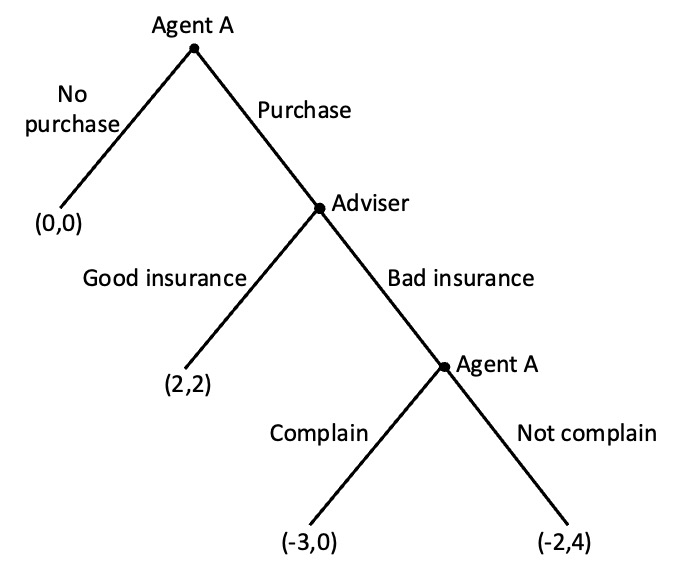
Agent A is going to their financial adviser to buy some life insurance. The adviser can sell them insurance that does not cover heart attacks but for which the adviser receives a huge sales commission (bad insurance). Or the adviser can sell Agent A comprehensive insurance for which their sales commission is lower (good insurance).
The payoffs (x,y) for each decision are indicated in the game tree below, with x being the satisfaction of Agent A and y being the satisfaction of the adviser.
a) Assume the adviser only cares about the payoffs indicated. What would the adviser do if Agent A chooses to purchase?
The adviser will compare payoffs of 4 for selling bad insurance and 2 for selling good insurance. They will choose to sell bad insurance.
b) What would Agent A do, anticipating the choice of the adviser?
Agent A will compare a payoff of 0 for no purchase and a payoff of -2 for purchase (knowing that they will be sold bad insurance). They will choose not to buy insurance.
c) Suppose now that Agent A can complain to the regulator if they are sold bad insurance. If Agent A is successful, they can cancel the insurance but would suffer a cost of -3 due to the effort involved. Would this change the outcome of the game?
Working by backward induction: Agent A has a choice between complaining for a payoff of -3 or not complaining for a payoff of -2. They do not complain.
The rest of the game plays out as per questions a) and b). There is no change to the outcome as they cannot commit to complain in advance (at least in this version of the game). The threat to complain is not credible.
d) Suppose Agent A has a reputation for seeking revenge and would experience satisfaction of +4 from complaining to the regulator (in addition to the effort cost of -3) as reciprocation for the action of the adviser. How would this change the outcome of the game?
The agent now has a choice between a payoff of 0 for selling bad insurance (as Agent A complains and the insurance is cancelled) and 2 for selling good insurance. They sell the good insurance.
Agent A now has a choice of a payoff of 0 for not purchasing insurance and 2 for purchasing. They make the purchase.