44 Game theory exercises
44.1 The cold war
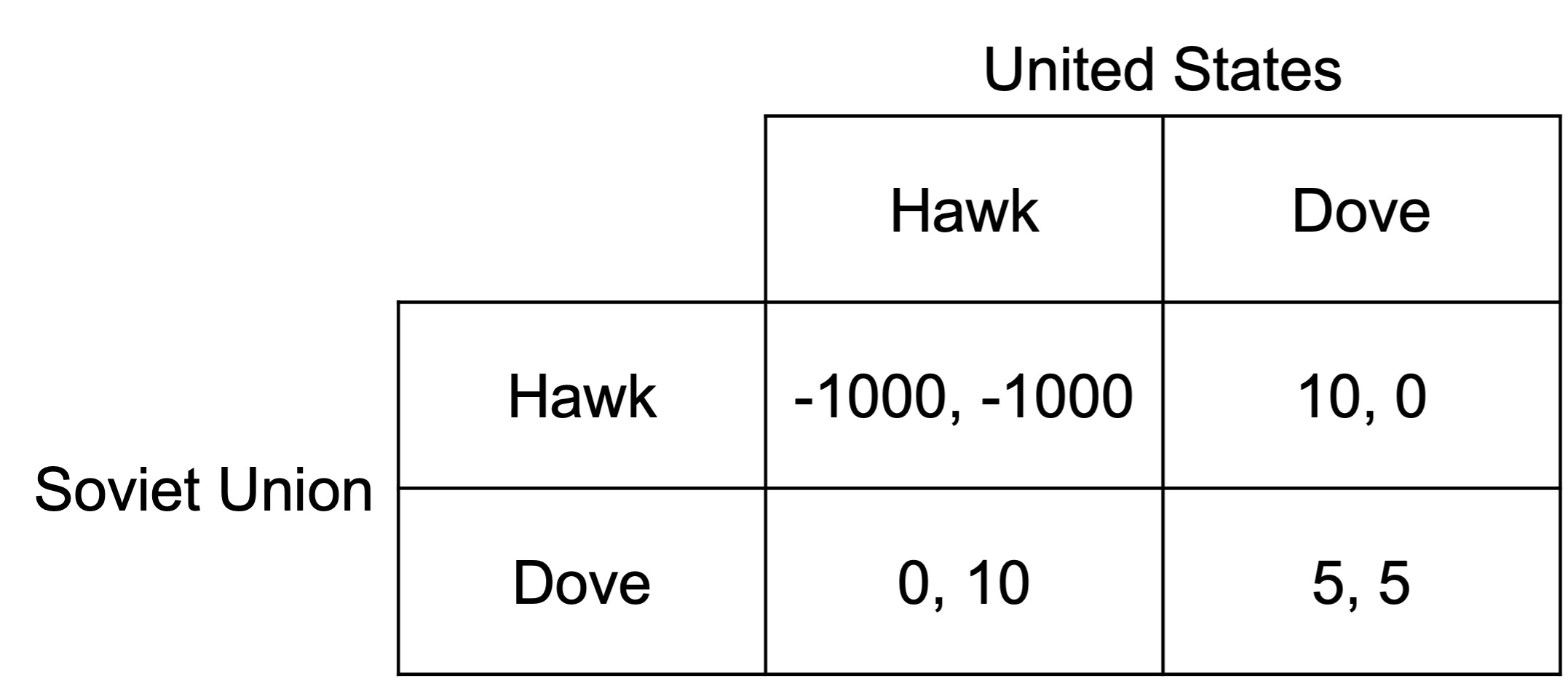
The year is 1964 and the Soviet Union and the United States are in the midst of the cold war.
Suppose each player is considering whether they should act aggressively (hawk) or peacefully (dove). If one plays hawk while the other plays dove, they win the cold war. If both play hawk, there is a nuclear armageddon.
The payoffs (x,y) of each option for the Soviet Union and United States is as follows:
a) What is the Nash equilibrium of this game? What other game does this resemble?
b) In the movie Dr Strangelove, the Soviet Union created a doomsday machine that would detonate automatically if there was a nuclear strike. The fallout would render the earth uninhabitable. The doomsday machine could not be deactivated and would explode if any attempt was made.
Explain how the doomsday device could act as a commitment device?
c) In the movie, the Soviet Union failed to inform the United States of the existence of the device. How could this failure to inform undermine its effectiveness as a commitment device?
A commitment will only be effective if it is both observable and irreversible. While the doomsday machine is irreversible, by not being observable it will not change the response of the United States. The United States will think they are playing the game analysed in part a), not that in part b).
44.2 Hiring
Robyn is hunting for a new employee. Robyn’s company uses highly-technical equipment and needs to invest heavily in training the new employee. If the new employee leaves straight after training, Robyn’s company will suffer a net loss from the employee. If the employee stays long-term, they will have a large gain.
Robyn approaches Sean and asks if he is interested in a long-term role with the company.
Sean is interested in the training as he could use it to boost his career, but sees less benefit in staying long-term. He considers whether he should say he is interested or not.
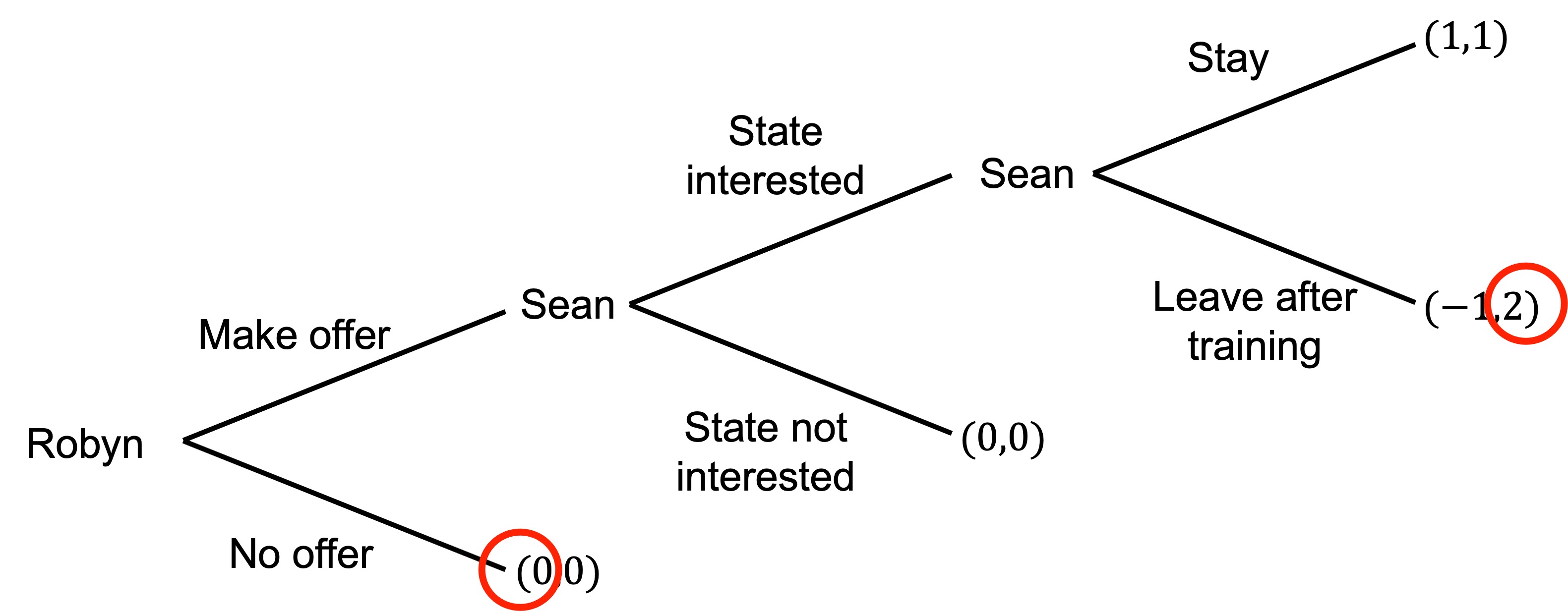
The extensive form of the game is laid out below, with the payoffs (x,y) being for Robyn and Sean respectively.
a) Will Robyn offer the position to Sean?
We work through the problem by backward induction.
Sean can get 2 by leaving after training or 1 by staying. He leaves after training.
When considering whether he will state that he is interested, he could get 2 for stating he is interested (as he will later leave) versus nothing for saying he is not interested. He states he is interested.
Robyn compares the -1 she gets for hiring Sean (as he will leave) with the zero for no offer. She does not make an offer.
The subgame-perfect equilibrium is (No offer; State interested, Leave after training).
b) What sort of strategic move could help John? What could make the move credible?
One option is to sign a binding contract with penalties if he leaves early. Any penalty greater than -1 would make staying more attractive.
A contract is both observable and irreversible (at least without mutual agreement).
44.3 Investment
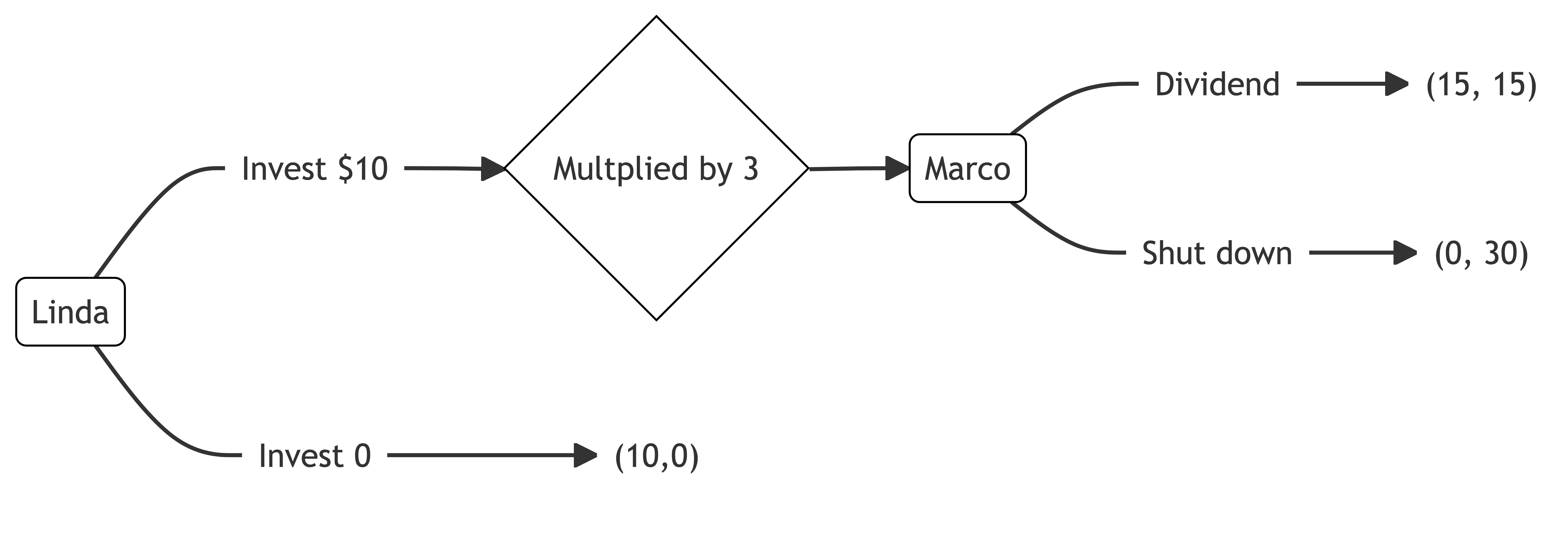
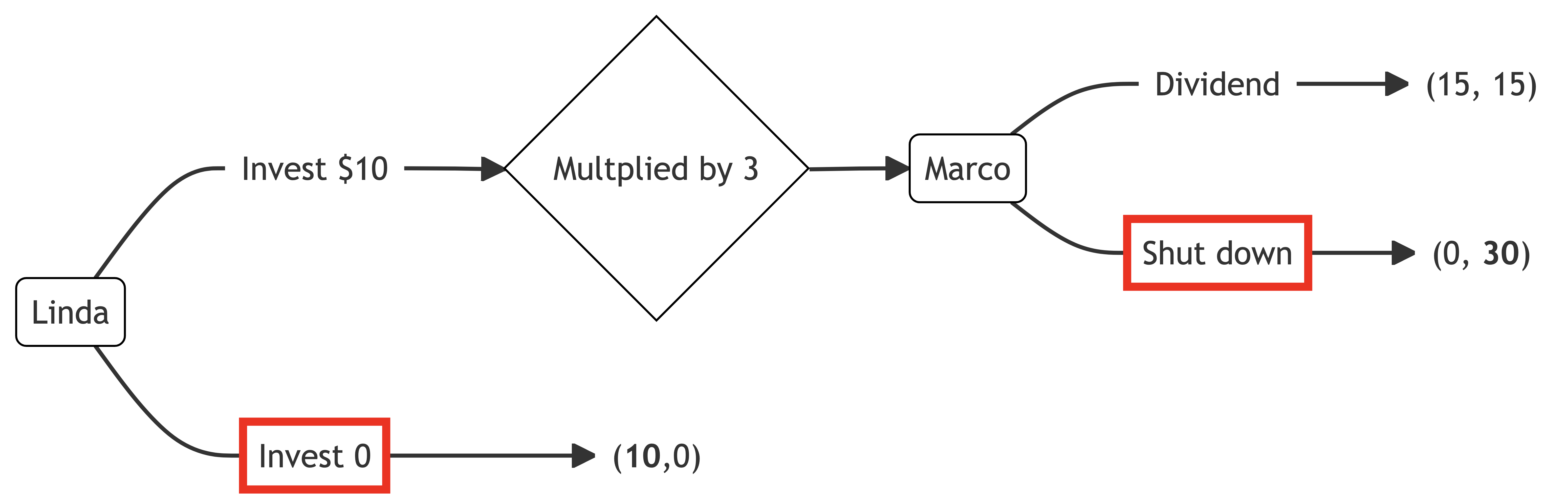
Linda is looking for investment opportunities. She identifies a promising crypto-based start-up created by Marco. Marco is looking for seed funding.
Linda can invest $10.
If Linda invests, her investment will triple in value. Marco can then decide to either shut down the start-up and keep the $30 or maintain the start-up in the market and pay a $15 dividend to each of Linda and himself.
If Linda does not invest, Linda keeps the $10. The start-up gets $0.
a) Draw the extensive form representation of the above sequential game.
b) What is the equilibrium of this game if Linda and Marco are purely self-interested?
44.4 War
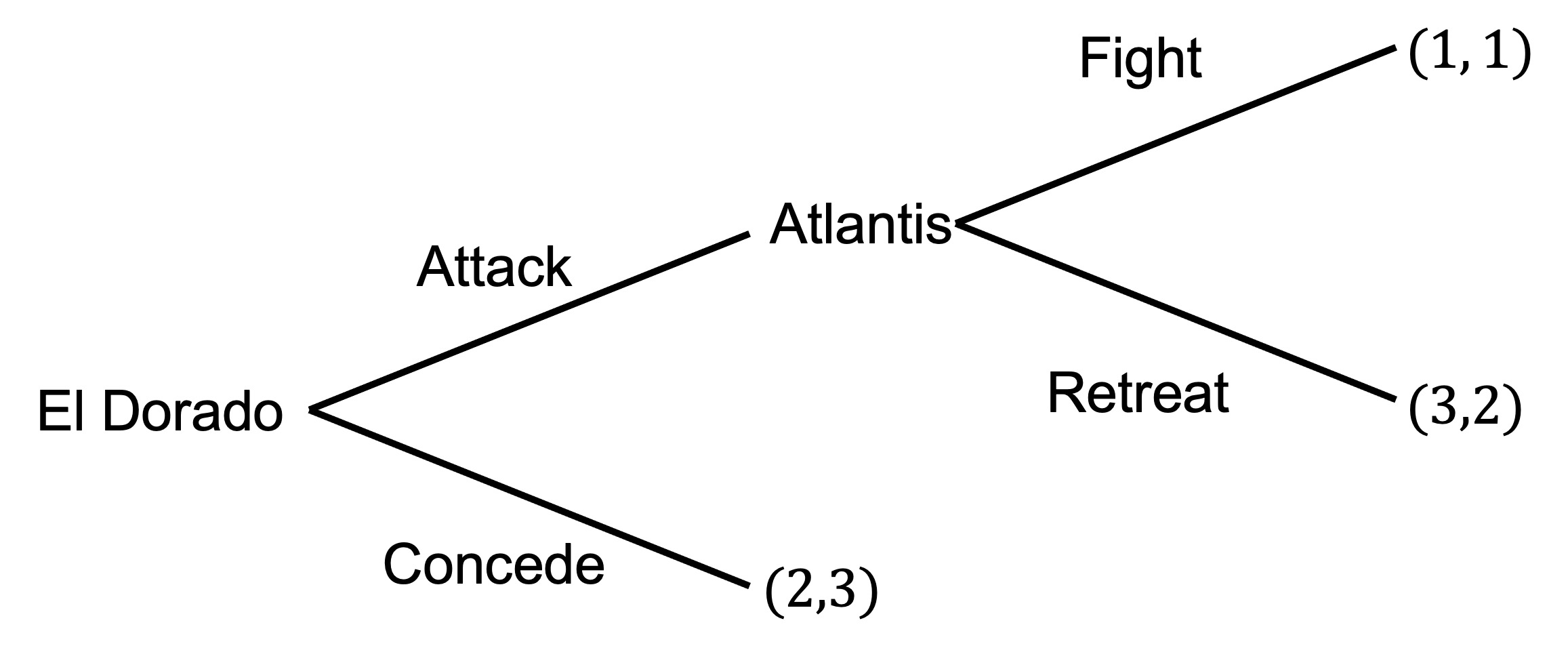
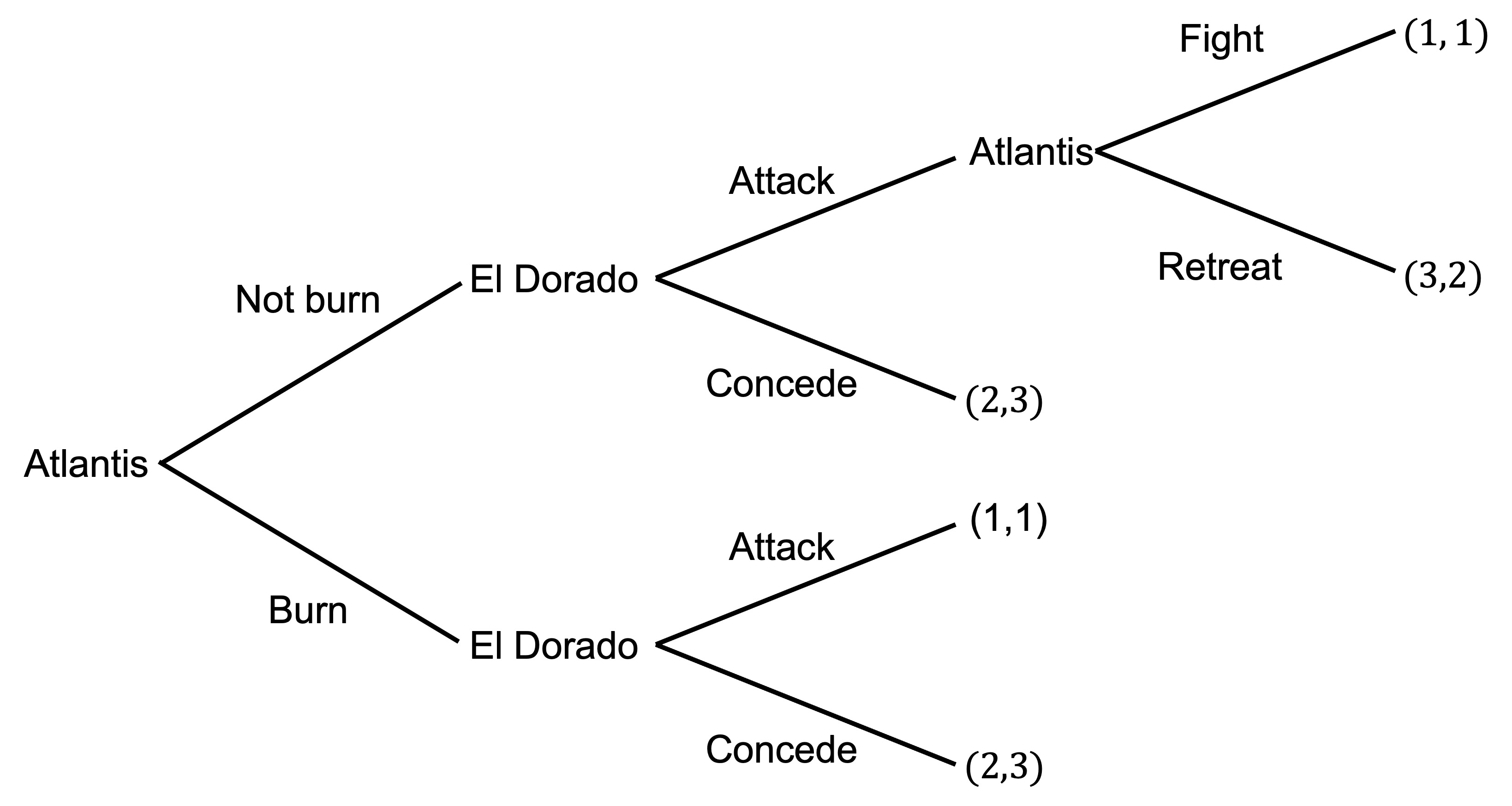
Two city states, Atlantis and El Dorado, are divided by a body of water. In the middle is an island that both states claim sovereignty over.
To establish their claims, both states have built a bridge to the island. Atlantis then sent troops to the island.
El Dorado is deciding whether to attack Atlantis’s troops to reclaim the island or to concede.
If El Dorado attacks, Atlantis need to decide whether to defend against the attack or to retreat back across the bridge.
If El Dorado attacks and Atlantis defends, both countries will suffer large losses.
These decisions and the payoffs (x,y) from each decision for El Dorado and Atlantis respectively are as follows.
a) What is the subgame-perfect equilibrium of this game?
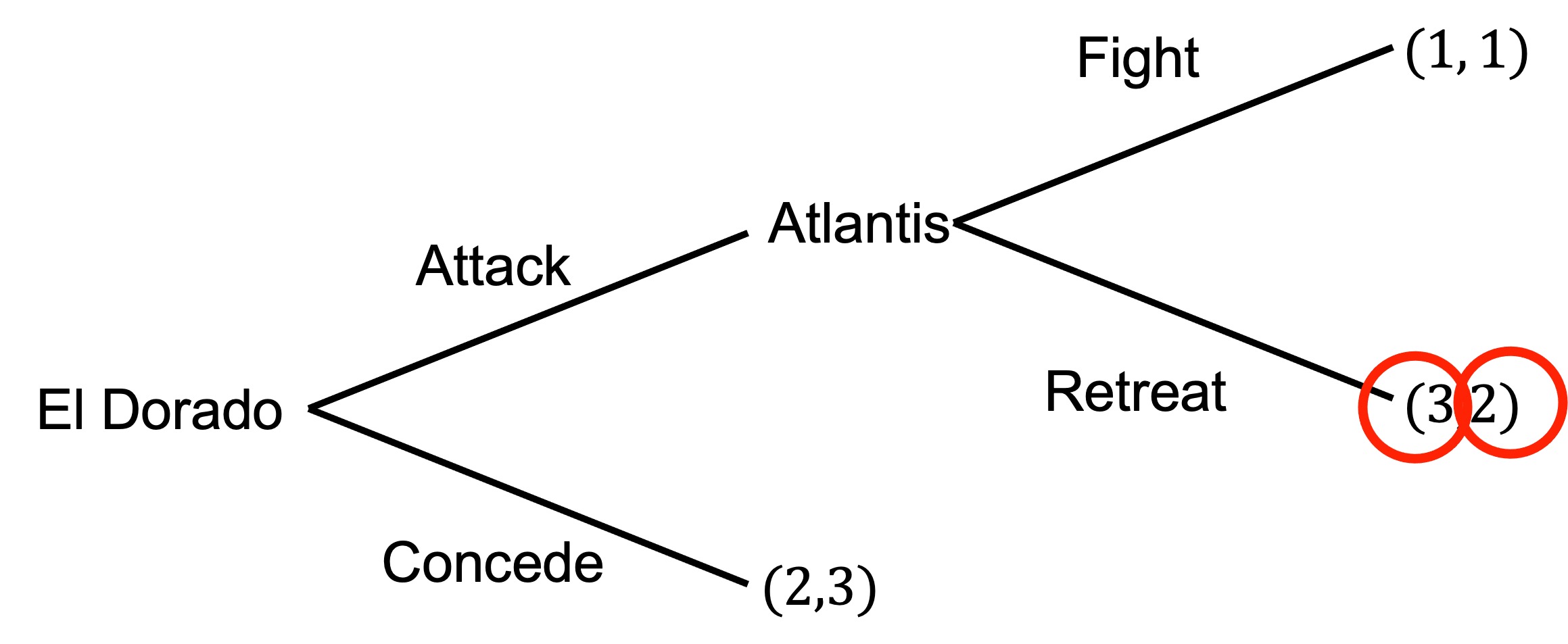
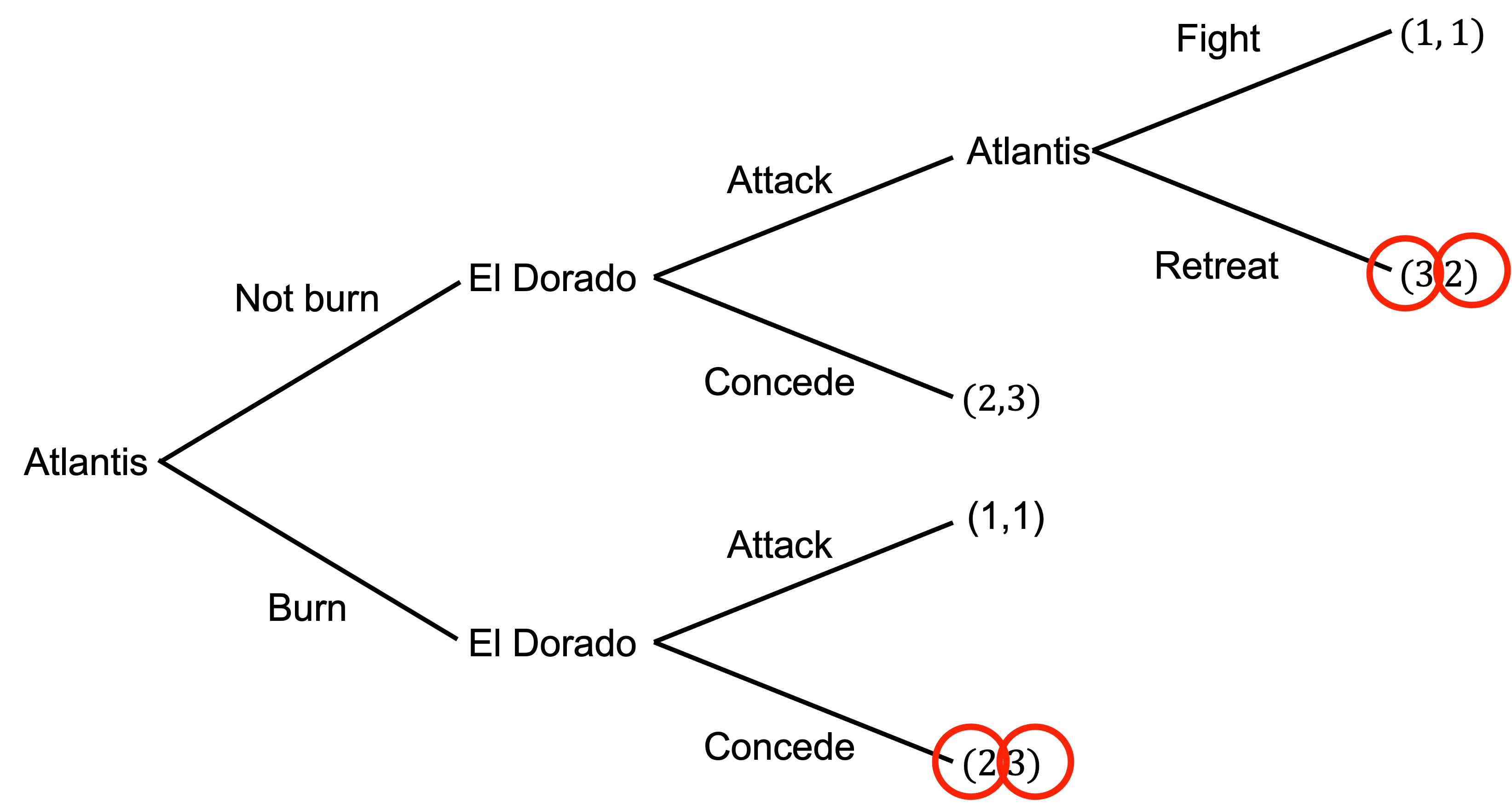
b) An adviser to the Atlantis army suggests that they burn the bridge behind them to remove the option of retreat.
Draw the new extensive form game that would emerge if Atlantis had the option of burning the bridge. What is the subgame-perfect equilibrium?
The new game is as follows (maintaining the payoffs as x,y for El Dorado and Atlantis respectively):
If we work through this game by backward induction, starting with the upper branch:
Atlantis would prefer to retreat (payoff of 2) compared to fighting (payoff of 1).
El Dorado would prefer to attack (payoff of 3) compared to conceding (payoff of 2).
For the lower branch:
- El Dorado would prefer to concede (payoff of 2) compated to attack (payoff of 1).
For Atlantis’s final decision, they would prefer to burn (payoff of 3) compared to not burning (payoff of 2).
Atlantis burns the bridge.
The subgame-perfect equilibrium is (Burn, Retreat; Attack, Concede).
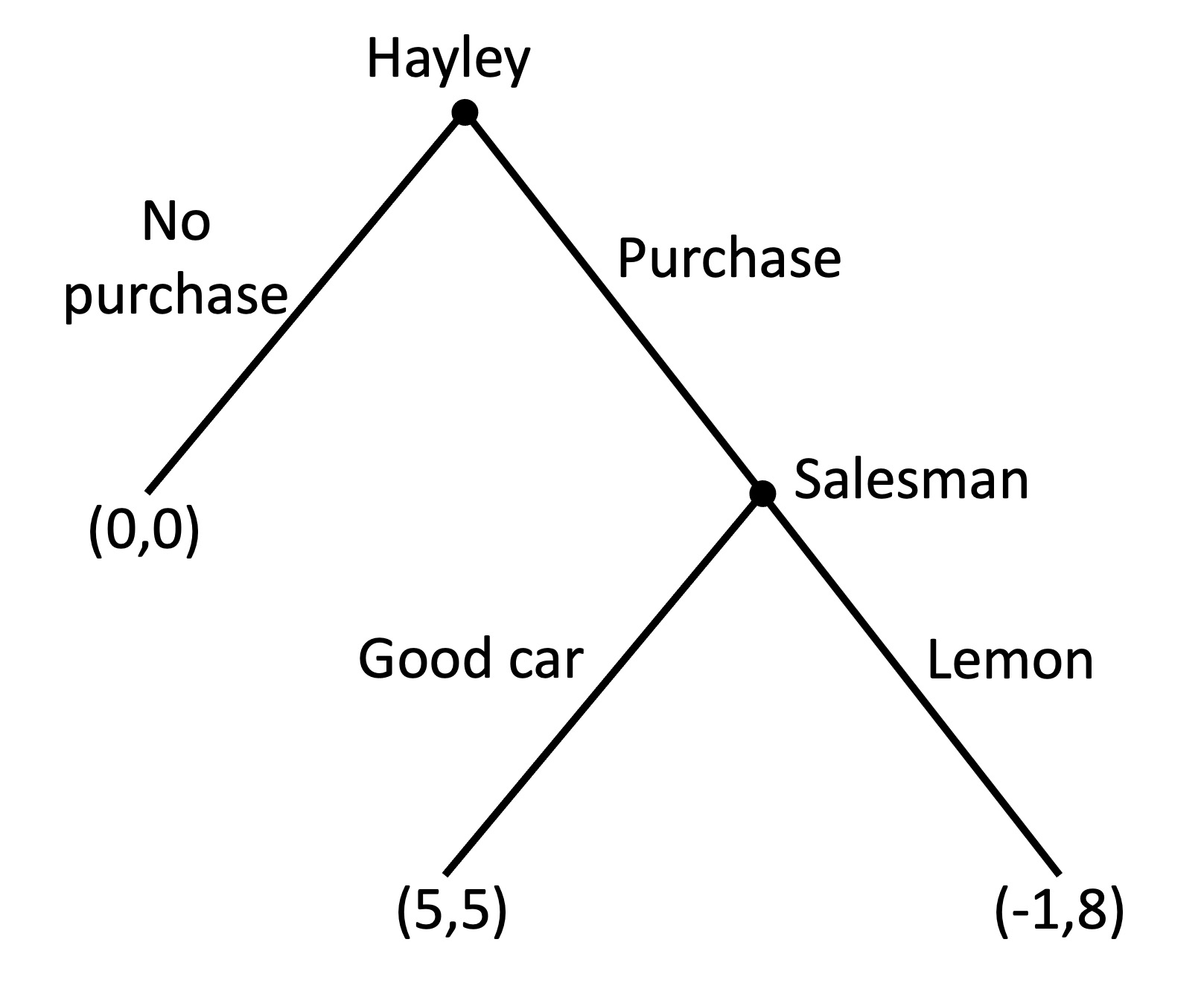
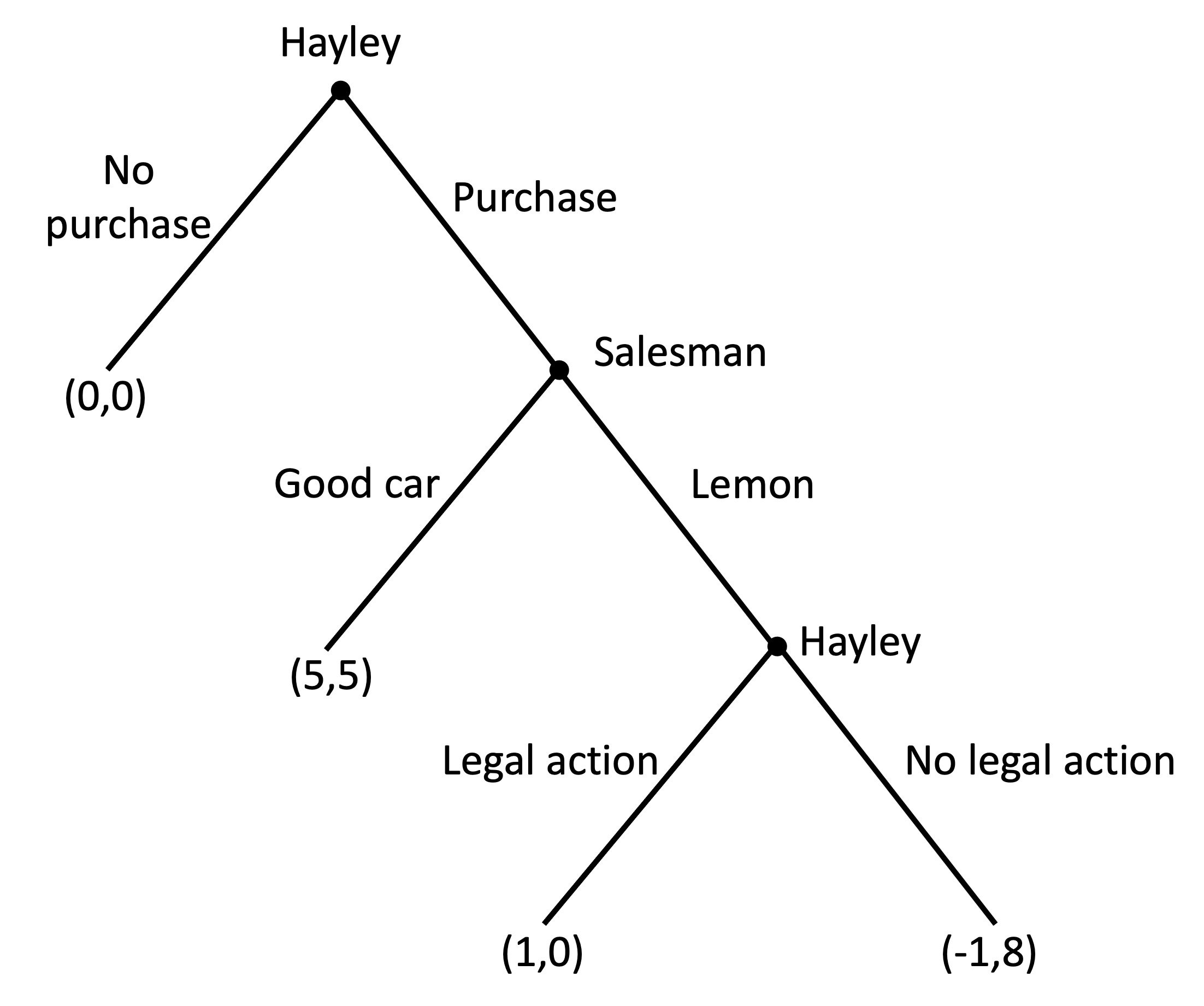
44.5 Buying a car
Hayley wants to buy a car. The used-car salesman can sell her a good car (for which he earns a small profit) or a lemon (for which he earns a large profit).
The payoffs (x,y) for each decision are indicated in the game tree below, with x being the Hayley’s satisfaction and y being the salesman’s profit.
a) Assume the salesman only cares about his profit. What would the salesman do if Hayley chooses to purchase? Why?
The salesman will compare payoffs of 8 for selling a lemon and 5 for selling a good car. He will choose to sell a lemon.
b) Given the anticipated choice of the salesman, would Hayley purchase the car? Why?
Hayley will compare a payoff of 0 for no purchase and a payoff of -1 for buying a car that will be a lemon. She chooses not to purchase.
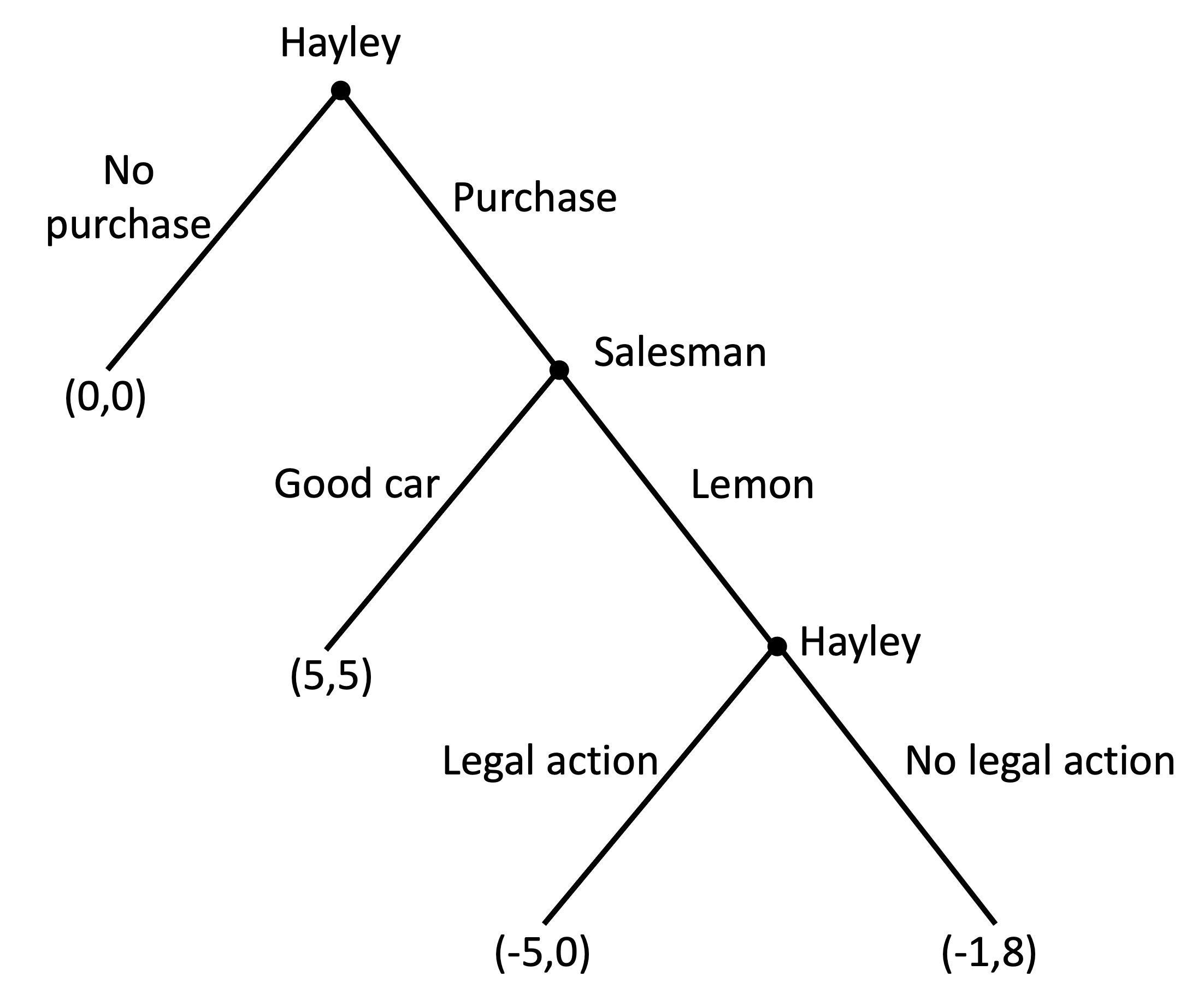
c) Suppose Hayley can take legal action if she is sold a lemon. If Hayley is successful in court, she will be refunded the purchase price but would suffer a cost of -5 due to the effort involved. Would this change the outcome? Why?
Working by backward induction, Hayley has a choice between taking legal action for a payoff of -5 or not complaining for a payoff of -1. She will not complain.
The rest of the game plays out as per questions a) and b). There is no change to the outcome as she cannot commit to complain in advance. The threat to take legal action is not credible.
d) Suppose Hayley has a reputation of being quick to anger and always carrying out her threats. Suppose Hayley would experience satisfaction of +6 from taking legal action (in addition to the effort cost of -5). The salesman knows this and believes it to be a credible commitment. Would this change the outcome? Why?
Hayley now has a choice between a payoff of 1 by taking legal action and a payoff of -1 for accepting the lemon. She would take legal action.
The salesman now has a choice between a payoff of 0 for selling the lemon (as Hayley takes legal action and the sale is refunded) and 5 for selling a good car. He sells the good car
Hayley now has a choice of a payoff of 0 for not purchasing a car, and 5 for purchasing. She makes the purchase and gets a good car.